What is an Angle?
Angles are formed between two rays extending from a single point:
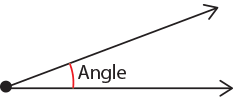
Angles are commonly drawn as an arc (part of a circle), as above.
Properties of Angles
Angles are measured in degrees, which is a measure of circularity, or rotation.
A full rotation, which would bring you back to face in the same direction, is 360°. A half-circle is therefore 180°, and a quarter-circle, or right angle, is 90°.
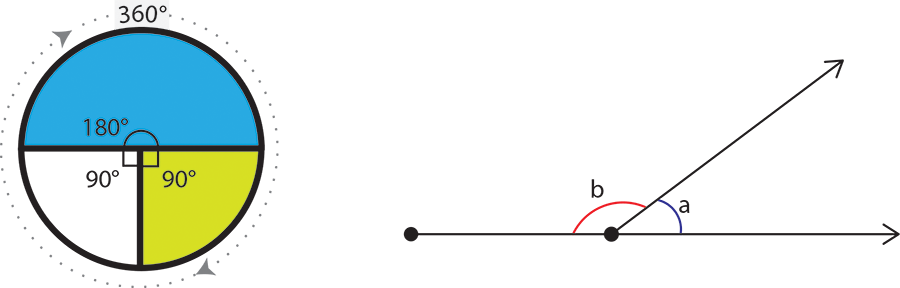
Two or more angles on a straight line add up to 180°. In the diagram above, the circle to the left is split into three sectors the angles of the green and white sectors are both 90°, adding up to 180°.
The figure to the right shows that angles a and b also add up to 180°. When you look at the diagram like this, it’s easy to see this, but it’s also surprisingly easy to forget in practice.
Naming Different Angles
An angle less than 90° is said to be acute, and one greater than 90° but less than 180° is obtuse.
An angle of exactly 180° is said to be straight. Angles greater than 180° are called reflex angles.
Different angles can be demonstrated on a clock face. The hour hand of the clock moves round as time passes through the day. The angle of the rotation is highlighted in green.

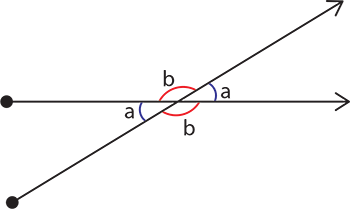
Opposite Angles: Intersecting Lines
When two lines intersect, the opposite angles are equal. In this case, not only are a and a the same, but, of course, a and b add up to 180°:
Intersections with parallel lines: a bit of a special case
Our page An Introduction to Geometry introduces the concept of parallel lines: lines that go on forever side by side and never cross, like railway lines.
The angles around any lines intersecting parallel lines also have some interesting properties.
If two parallel lines are intersected by a third straight line, then the angle at which the intersecting line crosses will be the same for both parallel lines.

The two angles a and the two angles b are said to be corresponding.
You will also immediately see that a and b add up to 180°, since they are on a straight line.
Angle c, which you will realise from the previous section is identical to a, is said to be alternate with a.
Read more at: https://www.skillsyouneed.com/num/angles.html
No comments:
Post a Comment