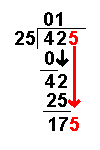
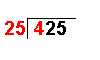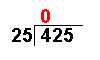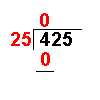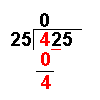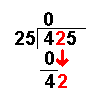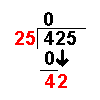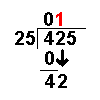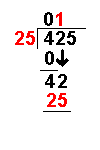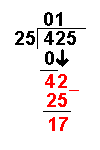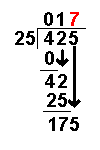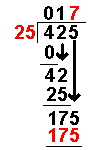This section is on the history of mathematicians. For a history of mathematics in general, see
History of mathematics

In 1938 in the United States, mathematicians were desired as teachers, calculating machine operators, mechanical engineers, accounting auditor bookkeepers, and actuary statisticians
One of the earliest known mathematicians was
Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed.
[1] He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to
Thales' Theorem.
The number of known mathematicians grew when
Pythagoras of Samos (c. 582–c. 507 BC) established the
Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number".
[2] It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins.
The first woman mathematician recorded by history was
Hypatia of Alexandria (AD 350 - 415). She succeeded her father as Librarian at the Great Library and wrote many works on applied mathematics. Because of a political dispute, the Christian community in Alexandria punished her, presuming she was involved, by stripping her naked and scraping off her skin with clamshells (some say roofing tiles).
[3]
Science and mathematics in the Islamic world during the Middle Ages followed various models and modes of funding varied based primarily on scholars. It was extensive patronage and strong intellectual policies implemented by specific rulers that allowed scientific knowledge to develop in many areas. Funding for translation of scientific texts in other languages was ongoing throughout the reign of certain caliphs,
[4] and it turned out that certain scholars became experts in the works they translated and in turn received further support for continuing to develop certain sciences. As these sciences received wider attention from the elite, more scholars were invited and funded to study particular sciences. An example of a translator and mathematician who benefited from this type of support was
al-Khawarizmi. A notable feature of many scholars working under Muslim rule in medieval times is that they were often polymaths. Examples include the work on
optics,
maths and
astronomy of
Ibn al-Haytham.
As time passed, many mathematicians gravitated towards universities. An emphasis on free thinking and experimentation had begun in Britain's oldest universities beginning in the seventeenth century at Oxford with the scientists
Robert Hooke and
Robert Boyle, and at Cambridge where
Isaac Newton was
Lucasian Professor of Mathematics & Physics. Moving into the 19th century, the objective of universities all across Europe evolved from teaching the “regurgitation of knowledge” to “encourag[ing] productive thinking.”
[5] In 1810, Humboldt convinced the King of Prussia to build a university in Berlin based on
Friedrich Schleiermacher’s liberal ideas; the goal was to demonstrate the process of the discovery of knowledge and to teach students to “take account of fundamental laws of science in all their thinking.” Thus, seminars and laboratories started to evolve.
[6]
British universities of this period adopted some approaches familiar to the Italian and German universities, but as they already enjoyed substantial freedoms and
autonomythe changes there had begun with the
Age of Enlightenment, the same influences that inspired Humboldt. The Universities of
Oxfordand
Cambridge emphasized the importance of
research, arguably more authentically implementing Humboldt’s idea of a university than even German universities, which were subject to state authority.
[7] Overall, science (including mathematics) became the focus of universities in the 19th and 20th centuries. Students could conduct research in
seminarsor
laboratories and began to produce doctoral theses with more scientific content.
[8]According to Humboldt, the mission of the
University of Berlin was to pursue scientific knowledge.
[9] The German university system fostered professional, bureaucratically regulated scientific research performed in well-equipped laboratories, instead of the kind of research done by private and individual scholars in Great Britain and France.
[10] In fact, Rüegg asserts that the German system is responsible for the development of the modern research university because it focused on the idea of “freedom of scientific research, teaching and study.”
[11]