complex numbers

A complex number can be visually represented as a pair of numbers (a, b)forming a vector on a diagram called an Argand diagram, representing the complex plane. "Re" is the real axis, "Im" is the imaginary axis, and isatisfies i² = −1.

A complex number is a number that can be expressed in the form a + bi, where a and bare real numbers, and i is a solution of the equation x² = −1, which is called an imaginary number because there is no real number that satisfies this equation. For the complex number a + bi, a is called the real part, and bis called the imaginary part. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers, and are fundamental in many aspects of our description of the natural world.^[1][2]

The complex number system can be defined as the algebraic extension of the ordinary real numbers by an imaginary number i.^[3] This means that complex numbers can be added, subtracted, and multiplied, as polynomials in the variable i, with the rule i² = −1 imposed. Furthermore, complex numbers can also be divided by nonzero complex numbers. Overall, the complex number system is a field.

Most importantly the complex numbers give rise to the fundamental theorem of algebra: every non-constant polynomial equation with complex coefficients has a complex solution. This property is true of the complex numbers, but not the reals. The 16th century Italian mathematician Gerolamo Cardano is credited with introducing complex numbers in his attempts to find solutions to cubic equations.^[4]

Geometrically, complex numbers extend the concept of the one-dimensional number lineto the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. The complex number a + bi can be identified with the point (a, b) in the complex plane. A complex number whose real part is zero is said to be purely imaginary; the points for these numbers lie on the vertical axis of the complex plane. A complex number whose imaginary part is zero can be viewed as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be represented in polar form, which associates each complex number with its distance from the origin (its magnitude) and with a particular angle known as the argumentof this complex number.

OverviewEdit

Complex numbers allow solutions to certain equations that have no solutions in real numbers. For example, the equation

${\displaystyle (x+1)^{2}=-9\,}$

has no real solution, since the square of a real number cannot be negative. Complex numbers provide a solution to this problem. The idea is to extend the real numbers with an indeterminate i (sometimes called the imaginary unit) that is taken to satisfy the relation i² = −1, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 + 3i and −1 − 3i, as can be verified using the fact that i² = −1:

${\displaystyle ((-1+3i)+1)^{2}=(3i)^{2}=(3^{2})(i^{2})=9(-1)=-9,}$

${\displaystyle ((-1-3i)+1)^{2}=(-3i)^{2}=(-3)^{2}(i^{2})=9(-1)=-9.}$

According to the fundamental theorem of algebra, all polynomial equations with real or complex coefficients in a single variable have a solution in complex numbers.

DefinitionEdit

An illustration of the complex plane. The real part of a complex number z = x + iy is x, and its imaginary part is y.

A complex number is a number of the form a + bi, where a and b are real numbers and i is an indeterminate satisfying i² = −1. For example, 2 + 3i is a complex number.^[5]

A complex number may therefore be defined as a polynomial in the single indeterminate i, with the relation i² + 1 = 0 imposed. From this definition, complex numbers can be added or multiplied, using the addition and multiplication for polynomials. Formally, the set of complex numbers is the quotient ring of the polynomial ring in the indeterminate i, by the ideal generated by the polynomial i² + 1(see below).^[6] The set of all complex numbers is denoted by ℂ, ${\displaystyle \mathbf {C} }$ or ${\displaystyle \mathbb {C} }$.

The real number a is called the real part of the complex number a + bi; the real number b is called the imaginary part of a + bi. By this convention, the imaginary part does not include a factor of i: hence b, not bi, is the imaginary part.^[7][8] The real part of a complex number z is denoted by Re(z) or ℜ(z); the imaginary part of a complex number z is denoted by Im(z) or ℑ(z). For example,

${\displaystyle {\begin{aligned}\operatorname {Re} (2+3i)&=2\\\operatorname {Im} (2+3i)&=3.\end{aligned}}}$

A real number a can be regarded as a complex number a + 0i whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi whose real part is zero. It is common to write a for a + 0i and bifor 0 + bi. Moreover, when the imaginary part is negative, it is common to write a − bi with b > 0 instead of a + (−b)i, for example 3 − 4iinstead of 3 + (−4)i.

Cartesian form and definition via ordered pairsEdit

A complex number can thus be identified with an ordered pair (Re(z),Im(z)) in the Cartesian plane, an identification sometimes known as the Cartesian form of z. In fact, a complex number can be defined as an ordered pair (a,b), but then rules for addition and multiplication must also be included as part of the definition (see below).^[9] William Rowan Hamilton introduced this approach to define the complex number system.^[10]

Complex planeEdit

Main article: Complex plane

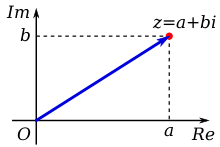
Figure 1: A complex number z, plotted as a point (red) and position vector (blue) on an Argand diagram; a+bi is its rectangular expression.

A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand diagram (see Pedoe 1988 and Solomentsev 2001), named after Jean-Robert Argand. The numbers are conventionally plotted using the real part as the horizontal component, and imaginary part as vertical (see Figure 1). These two values used to identify a given complex number are therefore called its Cartesian, rectangular, or algebraic form.

A position vector may also be defined in terms of its magnitude and direction relative to the origin. These are emphasized in a complex number's polar form. Using the polar form of the complex number in calculations may lead to a more intuitive interpretation of mathematical results. Notably, the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition while multiplication corresponds to multiplying their magnitudes and adding their arguments (i.e. the angles they make with the x axis). Viewed in this way the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin: (a+bi)i = ai+bi² = -b+ai.